HANDOUT
Family of Association Coefficients
(first part drawn from Zegers, F. E., & ten Berge, J. M. F. (1985). A
family of association coefficients for metric scales. Psychometrika,
50(1), 17-24 [PDF])
Assume that we are measuring the similarity between vector X and vector
Y. We use X* and Y* to refer to the canonical normalizations (or
uniformed versions) of X and Y.
Generic Measure of Similarity
If X* indicates the uniformed version of X, then Zegers & ten
Berge family of association measures can all be described by the
same equation:
All of these measures are normed to run between -1 and +1, where
the sign indicates the direction of association and the
magnitude indicates the strength of association
Can rescale a measure s that runs from -1 to +1 to run between 0
and 1 as follows:
(s +1)/2
Or, if a measure s runs between 0 and 1 and you want to rescale
to -1 to +1, use 2s-1
Absolute Scale Data
Identity coefficient. Scale differences not normalized away
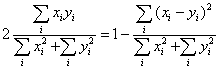
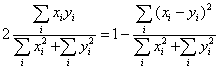
Ratio Scale Data
Tucker's congruence = coefficient of proportionality.
Differences in amplitude normalized away
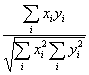
Additive Scale Data
Coefficient of additivity = Winer's I
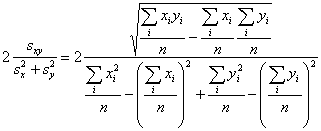
Interval Scale Data
Pearson correlation = coefficient of linearity
Ordinal data
Spearman's rho = r(X*,Y*)
Goodman and Kruskal Gamma = (P - Q)/(P + Q), P is concordant
pair and Q is discordant
example:
| |
X |
Y |
|
1 |
1 |
1 |
|
2 |
1 |
2 |
|
3 |
2 |
1 |
|
4 |
2 |
1 |
|
5 |
3 |
1 |
|
6 |
3 |
1 |
|
7 |
3 |
2 |
| |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1 |
|
n |
n |
n |
n |
n |
p |
|
2 |
|
|
q |
q |
q |
q |
n |
|
3 |
|
|
|
n |
n |
n |
p |
|
4 |
|
|
|
|
n |
n |
p |
|
5 |
|
|
|
|
|
n |
n |
|
6 |
|
|
|
|
|
|
n |
|
7 |
|
|
|
|
|
|
|
P = 3, Q = 4, gamma = -1/7
Or do it via contingency table:
P = 1*(0+1) + 2*(1) = 3
Q = 1*(2+2) +0*(2) = 4
Gamma = -1/7
Another example:
|
City Size/Arenas |
Small |
Medium |
Large |
|
Weak Mayor |
a = 10 |
b = 5 |
c = 2 |
|
Strong Mayor |
d = 10 |
e = 15 |
f = 20 |
P = a(e+f) + bf = 10(15+20) + 5*20 = 450
Q = c(d+e) + bd = 2(10+15) + 5*10 = 100
gamma = (P - Q)/(P + Q) = (450-100)/(450 + 100) = .636
Presence/Absence Data
Simple matches
Jaccard
Gamma / Yule's Q
(ad-bc)/(ad+bc)
(OR-1)/(OR+1)
Nominal Data
chi-square
cramer's v
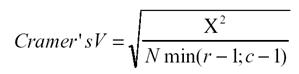
(equals phi when table is 2 by 2 |
