EXERCISE

Density Tables

Overview

Density tables provide a way to examine the number of ties within and between categories of nodes. For example, you might look at the ties between members of different departments in an organization.

Data

For this exercise, we will be using the maydata.xls datafile.

Creating the UCINET Datasets

The maydata.xls is, obviously an Excel file. First step is to open the file in Excel (not in UCINET) and navigate to the concoinfo tab. Highlight all cells and copy to the clipboard. Now start up UCINET, open the ucinet spreadsheet, and paste the contents of the clipboard into the spreadsheet. (Make sure cursor is pointing to top left cell first, up in the shaded area.) Save the data as CONCOINFO.

Now flip back to Excel and click on the concattr tab. Highlight the data (down to row 47 only) and copy to clipboard. In UCINET spreadsheet, clear the spreadsheet if necessary by pressing New button and paste the data into top left cell. Save this as CONCOATTR.

Now check on your work by exiting the ucinet spreadsheet and pressing the Display button on the main menu (the big "D"). Select CONCOINFO and examine the results. Repeat with CONCOATTR.

Notice that the first data column of concoattr is gender, the second is prac (practice -- like a person's area of expertise), the third is region, and the fourth is City.

Now for an important bit. The network data, concoinfo, actually contain ordinal values from one to five indicating strength of tie. For this exercise, we want to look at only strong ties. So we will dichotomize the data such that we have a tie if the strength is greater than 3 and no tie otherwise.

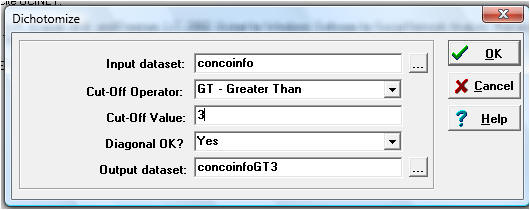
To do this, go to transform|dichotomize and select concoinfo as the input dataset, and 3 as the cutoff value. Let the output dataset be called "concoinfogt3", like this:

Verify the data by running Display and checking that you only have zeros and ones now.

Running Density

From the main menu go to networks|cohesion|density|density by groups. For "network dataset" select concoinfogt3. For "row partition" select concoattr. It should automatically choose the first column of concoattr which is gender. For "column partition", enter the same as for row partition. Down below, where it says "method", choose "sum".

The key output is this table:

This indicates that there are 8 strong ties from women to women (women are code 0), 15 ties from women to men, and so on.

If we had chosen "Average" for the method instead of sum, we would have gotten this:

These are proper densities and indicate the number of ties between/within groups as a function of the number possible (i.e., the number of pairs in which the first person belongs to one group and the other belongs to the other). So, among women, around 7% of all possible strong ties are actually realized, and among men, around 10% of possible ties are actually present.

Running Density Again

The attribute dataset concoattr contains more than just gender. There is also Gender Prac(tice) Region and City. Try running density by groups for each of these attributes. Which attribute seems to really make a difference in terms of patterning who has strong ties to whom?

Statistical Testing

Are the differences in densities in the table above for gender big differences? Are they statistically significant? There are many ways to test this.

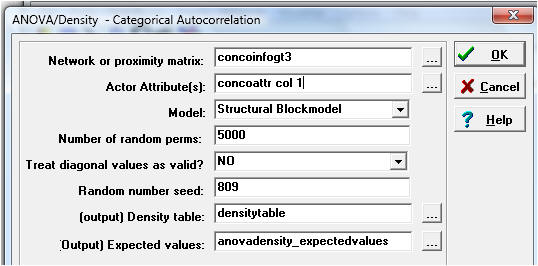
Let's begin by running something called "anova density models". From the ucinet main menu go to tools|testing hypotheses|mixed dyadic/nodal|categorical|anova density models. For "network or proximity matrix:" use concoinfogt3. For "actor attributes" use "concoattr col 1". For model, leave the default choice which is "structural blockmodel". Like this:

The key output will be this:

The important result is that the r-square is low, and the p-value is 0.06 which is not really significant. So the differences in densities in the four blocks of the density table could have happened by chance.

The regression coefficients table gives the coefficients for the variables. The variables are dummy variables that correspond to the four blocks in the density table. So the 1-1 variable refers to ties between women and women, the 1-2 variable codes ties from women to men, the 2-1 variables indicates ties from men to women, and the intercept stands in for the ties from men to men (the reference category). The unstandardized coefficients for the three variables can be interpreted as offsets from the baseline value given by the intercept. So the -0.0306 for women-women ties indicates that women have fewer ties to other women than the reference category (men to men). In fact, subtracting 0.0306 from 0.1034 gives the density for the women-women cell, which is 0.0727 according to our table above. I advise not interpreting the significance of the coefficients, at least not without some Bonferroni-type adjustment for simultaneous tests.