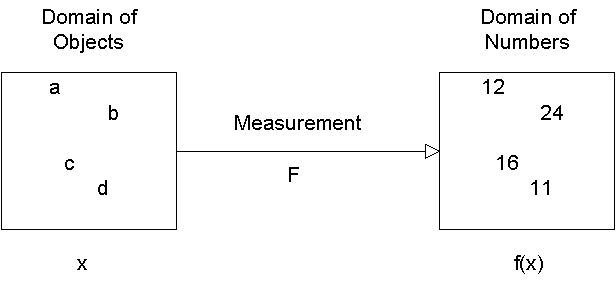
Measurement is the assignment of numbers to objects in such a way that physical relationships and operations among the objects correspond to arithmetic relationships and operations among the numbers.

Both objects and relationships are mapped: All measurement is a form of modeling; it embodies a primitive theory of how the objects work.
A function is a mapping of the objects in one set to the objects in another. The two sets can be the same. For example, the function Y = X2 is a mapping of real numbers to real numbers. We use the notation f(x) = x2 to define a function. You can think of f(x) as saying "a function of x". The right hand side of the equation defines exactly what function of x it is.
Different levels of measurement are defined by the number and kind of correspondences that hold between the physical relations among objects and the arithmetic relations among the scores.
Consider the example of measuring mass or weight. When we measure weight, two objects that weigh the same are assigned the measured value, or score. Hence, the relationship among objects is mirrored by equality of numbers.
Similarly, if two objects balance each other on a balance scale, our system of measurement assigns the same weight to each. hence the operation of balancing maps to equality.
Suppose two items x and y are placed together on left of scale. the measured weight of the two combined is equal to the sum of scores of each individual item
Suppose f(x) = 5. Then five x's will weight 5*f(x) = 25. So multiplication of measured scores by constant maps to physical operation of putting that many items on the scale.
But not all mathematical relationships have a counterpart in the levels. the log of f(x) means nothing in weight land. The breakdown of f(x) into its prime multipliers means nothing. if one measured is the log of another, this implies no particular relationship among the objects.
The different levels of measurement are distinguished by which arithmetic operations on the measured scores have counterparts in physical operations on the objects.
to put it another way, levels of measurement are distinghished by which arithmetic ops on the scores are meaningful
in fact, in a deep sense, the theory of measurement is a theory of meaningfulness -- this will become very clear in about 30 minutes.
as an aside i would point out that any time we talk about meaning, we are talking about some kind of mapping from one system to another. To understand something is to build a model of it, it is to translate it into different terms.
The rules that distinguish different scales of measurement also define the uniqueness of measurement: the number and kind of alternative measurements that are valid
what i'm talking about is the existence of things like alternative units
for example, if i can measure height in meters (i'm 1.73 meters tall), then I can also measure it in centimeters (173) or inches (68). These are all equally valid.
i'll make this clearer soon.
in nominal measurement, we assign numeric scores in such a way that only equality of scores has meaning for the attribute being measured
e.g. measure weight on nominal scale. suppose that in my system of measurement, my weight is assigned a "12". now suppose we compare my weight to yours. If you also were assigned a 12, this would mean that we both had the same weight. But if you had any other score, there is nothing we could say.
if you have a 16, it does not mean you weigh more than i do.
so in nominal scale, the only physical property preserved or captured by the numeric scores, is equality. x same weight y iff f(x) = f(y)
note the tremendous lack of uniqueness of measurement scales: any other number system that preserved that property would be ok
in order to tell whether two sets of measurements are the same, you need to recode both of them so they use the same codes, then compare them: the fact that they initially have different values doesn't mean anything.
ordinal
in ordinal measurement, we assign numeric scores in such a way that not only equality of scores but ordinality of scores have meaning for the attribute being measured
e.g. measure weight on ordinal scale. suppose that in my system of measurement, my weight is assigned a "12". now suppose we compare my weight to yours.
If you also were assigned a 12, this would mean that we both had the same weight.
But if you had a 24, this would mean that we not only had different weights, but you weigh more than I do.
However, we can't say how much more you weigh than I do. for example if A weights 12 and B weighs 16 and C weighs 24, we cannot say that the difference in weight between A and B is half of what the difference between B and C is.
so in ordinal scale, the only physical properties preserved or captured by the measured scores is equality and ordinality:
if A weighs same as B then f(a) = f(b) and vice versa
if A weighs more than B then f(a) > f(b) and vice versa
again, any method of assigning numeric scores that satisfies these two rules is valid, which means that ordinal measurements are unique up to a monotone transofmration
in order to tell whether two sets of measurements are the same, you need to rank order both sets and then compare them: the fact that they initially have different values doesn't mean anything.
interval
in interval measurement, we assign numeric scores in such a way that not only equality and ordinaly of scores have meaning, but also the intervals between the scores.
e.g. measure weight on an interval scale. suppose that in my system of measurement, my weight is assigned a "12". now suppose we compare my weight to yours.
If you also were assigned a 12, this would mean that we both had the same weight.
But if you had a 24, this would mean that we not only had different weights, but you weigh more than I do.
Furthermore, if A weighs 12 and B weighs 16 and C weighs 24, we can say that the difference in weight between A and B is half of what the difference between B and C is. the difference between numbers has meaning now.
however, we still can't say that if f(A) is 12 and f(C) is 24, that C weighs twice as much as A.
as proof, consider temperature of two cities, measured in degrees fahrenheit. city A is 80 degrees and city B is 40 degrees. We are tempted to say city A is twice as hot. But suppose we measure temperature in centigrade. You know that to get from fahrenheit to centigrade we subtract 32 and multiply by 5/9ths. So city A is 27 degress centigrade. City B is 4 degrees centigrade. It no longer appears to be twice as hot: more like 7 times as hot. Now you know both centigrade and fahrenheit are equally valid measuring scales of temperature. But they are interval measures, and it is not meaningful to say that something is twice something else when you measure on an interval scale.
so in interval scale, the only physical properties preserved or captured by the measured scores are equality, ordinality, and interval size
if A weighs same as B then f(a) = f(b) and vice versa
if A weighs more than B then f(a) > f(b) and vice versa
if the difference between A and B is twice as big as difference between A and C, then 2*(f(a)-f(c)) = f(a)-f(b)
any method of assigning numeric scores that satisfies these three rules is valid, and this turns out to mean that interval measurements are unique up to a linear transofmration of the values.
a linear transform is one that looks like this: g(x) = m*f(x) - b where m and b are constants. the transformation from fahrenheit to centigrade is the like this: C = (F-32)*5/9 = 5/9F - 17.7-
in order to tell whether two sets of measurements are the same, you need to standardize both of them and then compare them: the fact that they initially have different values doesn't mean anything.
to standardize, subtract mean and divide by standard deviation.
ratio
in ratio-scale measurement, we assign numeric scores in such a way that not only equality and ordinality and the intervals between the scores have meaning, but also ratios of the scores.
e.g. measure weight on a ratio scale. suppose that in my system of measurement, my weight is assigned a "12". now suppose we compare my weight to yours.
If you also were assigned a 12, this would mean that we both had the same weight.
But if you had a 24, this would mean that we not only had different weights, but you weigh more than I do.
Furthermore, if A weighs 12 and B weighs 16 and C weighs 24, we can say that the difference in weight between A and B is half of what the difference between B and C is. the difference between numbers has meaning.
and, if your measured weight is 24 and my measured weight is 12, then we can say that you weigh twice as much as I do.
so in ratio scale, the following properties are preserved by the measured scores:
if A weighs same as B then f(a) = f(b) and vice versa
if A weighs more than B then f(a) > f(b) and vice versa
if the difference between A and B is twice as big as difference between A and C, then 2*(f(a)-f(c)) = f(a)-f(b)
if A has twice the mass as B, then f(a) = 2*(f(b) and vice versa
any method of assigning numeric scores that satisfies these four rules is valid, and this turns out to mean that ratio measurements are unique up to a congruence or proportionality transformation of the values.
a congruence transform is one that looks like this: g(x) = m*f(x) where m is a constant.
in order to tell whether two sets of measurements are the same, you need to normalize both of them and then compare them: the fact that they initially have different values doesn't mean anything.
to normalize ratio variables, divide each value by sqrt of sum of squares.